前言
先看一个问题
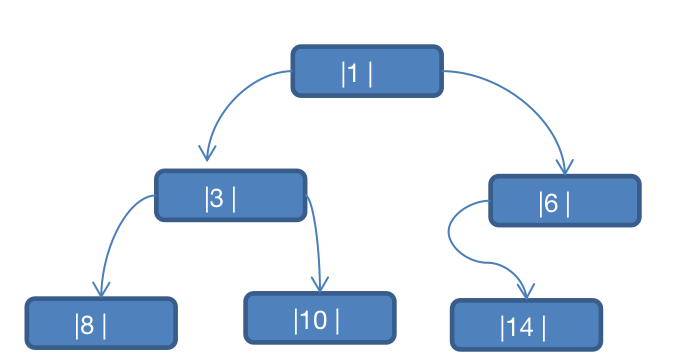
将数列 {1, 3, 6, 8, 10, 14 } 构建成一颗二叉树. n+1=7
问题分析:
- 当我们对上面的二叉树进行中序遍历时,数列为 {8, 3, 10, 1, 6, 14 }
- 但是 6, 8, 10, 14 这几个节点的 左右指针,并没有完全的利用上.
- 如果我们希望充分的利用 各个节点的左右指针, 让各个节点可以指向自己的前后节点,怎么办?
- 解决方案-线索二叉树
线索二叉树基本介绍
-
n个结点的二叉链表中含有n+1 【公式 2n-(n-1)=n+1】 个空指针域。利用二叉链表中的空指针域,存放指向该结点在某种遍历次序下的前驱和后继结点的指针(这种附加的指针称为"线索")
-
这种加上了线索的二叉链表称为线索链表,相应的二叉树称为线索二叉树(Threaded BinaryTree)。根据线索性质的不同,线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种
-
一个结点的前一个结点,称为前驱结点
-
一个结点的后一个结点,称为后继结点
线索二叉树应用案例
思路分析: 中序遍历的结果:{8, 3, 10, 1, 14, 6}

说明: 当线索化二叉树后,Node节点的 属性 left 和 right ,有如下情况:
- left 指向的是左子树,也可能是指向的前驱节点. 比如 ① 节点 left 指向的左子树, 而 ⑩ 节点的 left 指向的就是前驱节点.
- right指向的是右子树,也可能是指向后继节点,比如 ① 节点right 指向的是右子树,而⑩ 节点的right 指向的是后继节点.
遍历线索化二叉树
说明:对前面的中序线索化的二叉树, 进行遍历
分析:因为线索化后,各个结点指向有变化,因此原来的遍历方式不能使用,这时需要使用新的方式遍历线索化二叉树,各个节点可以通过线型方式遍历,因此无需使用递归方式,这样也提高了遍历的效率。 遍历的次序应当和中序遍历保持一致。
代码实现
节点
/**
* 树节点
*/
class Node{
private int no;
private String name;
private Node leftNode;
private Node rightNode;
/**
* 0表示指向左子树 ,1 表示指向前驱节点
*/
private int leftNodeType;
/**
* 0表示指向右子树, 1表示指向后继节点
*/
private int rightNodeType;
public int getLeftNodeType() {
return leftNodeType;
}
public int getRightNodeType() {
return rightNodeType;
}
public void setLeftNodeType(int leftNodeType) {
this.leftNodeType = leftNodeType;
}
public void setRightNodeType(int rightNodeType) {
this.rightNodeType = rightNodeType;
}
public Node(int no, String name) {
this.no = no;
this.name = name;
}
public void setNo(int no) {
this.no = no;
}
public void setName(String name) {
this.name = name;
}
public void setLeftNode(Node leftNode) {
this.leftNode = leftNode;
}
public void setRightNode(Node rightNode) {
this.rightNode = rightNode;
}
public int getNo() {
return no;
}
public String getName() {
return name;
}
public Node getLeftNode() {
return leftNode;
}
public Node getRightNode() {
return rightNode;
}
@Override
public String toString() {
return "Node{" +
"no=" + no +
", name='" + name + '\'' +
'}';
}
}
/**
* 线索化二叉树
*/
public class TheadBinaryTree {
private Node root;
private Node pre;
public TheadBinaryTree(Node root){
this.root=root;
}
public void theadBinaryTreeNodes(){
this.theadBinaryTreeNodes(root);
}
/**
* 线索化二叉树 遍历
*/
public void theadBinaryTreeNodeList(){
Node node=root;
while (node !=null){
while (node.getLeftNodeType() == 0){
node=node.getLeftNode();
}
System.out.println(node);
while (node.getRightNodeType() == 1){
node= node.getRightNode();
System.out.println(node);
}
node=node.getRightNode();
}
}
/**
* 线索化二叉树
* @param node
*/
public void theadBinaryTreeNodes(Node node){
if (node == null){
return;
}
theadBinaryTreeNodes(node.getLeftNode());
if (node.getLeftNode() == null){
node.setLeftNode(pre);
node.setLeftNodeType(1);
}
if (pre!=null&&pre.getRightNode() == null){
pre.setRightNode(node);
pre.setRightNodeType(1);
}
pre=node;
theadBinaryTreeNodes(node.getRightNode());
}
public static void main(String[] args) {
Node root = new Node(1, "a");
Node node2= new Node(3, "b");
Node node3 = new Node(6, "c");
Node node4 = new Node(8, "d");
Node node5 = new Node(10, "e");
Node node6 = new Node(14, "e");
root.setLeftNode(node2);
root.setRightNode(node3);
node2.setLeftNode(node4);
node2.setRightNode(node5);
node3.setLeftNode(node6);
TheadBinaryTree theadBinaryTree = new TheadBinaryTree(root);
theadBinaryTree.theadBinaryTreeNodes();
System.out.println(node4.getRightNode());
theadBinaryTree.theadBinaryTreeNodeList();
}
}


评论区