看一个案例(说明二叉排序树可能的问题)
给你一个数列{1,2,3,4,5,6},要求创建一颗二叉排序树(BST), 并分析问题所在.
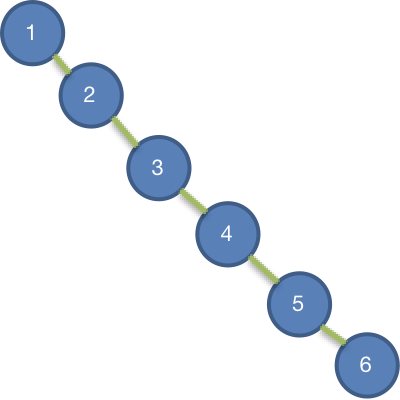
存在的问题分析:
- 左子树全部为空,从形式上看,更像一个单链表.
- 插入速度没有影响
- 查询速度明显降低(因为需要依次比较), 不能发挥BST 的优势,因为每次还需要比较左子树,其查询速度比 单链表还慢
- 解决方案-平衡二叉树(AVL)
基本介绍
-
平衡二叉树也叫平衡二叉搜索树(Self-balancing binary search tree)又被称为AVL树, 可以保证查询效率较高。
-
具有以下特点:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。
-
平衡二叉树的失衡调整主要是通过旋转最小失衡子树来实现的。根据旋转的方向有两种处理方式,左旋 与 右旋 。
-
旋转的目的就是减少高度,通过降低整棵树的高度来平衡。哪边的树高,就把那边的树向上旋转。
代码实现
节点对象
class Node{
int value;
Node left;
Node right;
public Node(int value){
this.value=value;
}
// 返回左子树的高度
public int leftHeight() {
if (left == null) {
return 0;
}
return left.height();
}
// 返回右子树的高度
public int rightHeight() {
if (right == null) {
return 0;
}
return right.height();
}
// 返回 以该结点为根结点的树的高度
public int height() {
return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
}
//左旋转方法
private void leftRotate() {
//创建新的结点,以当前根结点的值
Node newNode = new Node(value);
//把新的结点的左子树设置成当前结点的左子树
newNode.left = left;
//把新的结点的右子树设置成带你过去结点的右子树的左子树
newNode.right = right.left;
//把当前结点的值替换成右子结点的值
value = right.value;
//把当前结点的右子树设置成当前结点右子树的右子树
right = right.right;
//把当前结点的左子树(左子结点)设置成新的结点
left = newNode;
}
//右旋转
private void rightRotate() {
Node newNode = new Node(value);
newNode.right = right;
newNode.left = left.right;
value = left.value;
left = left.left;
right = newNode;
}
/**
* 根据value查询节点的父节点
* @param value
* @return
*/
public Node searchParent(int value){
if ((this.left!=null&& this.left.value == value)||
(this.right!=null&&this.right.value==value)){
return this;
}else {
if (value<this.value&&this.left!=null){
return this.left.searchParent(value);
}else if (value>=this.value&&this.right!=null){
return this.right.searchParent(value);
}else {
return null;
}
}
}
/**
* 根据value查找节点
* @param value
* @return
*/
public Node search(int value){
if (value == this.value){
return this;
}else if (value < this.value){
if (this.left == null ){
return null;
}
return this.left.search(value);
}else {
if (this.right == null ){
return null;
}
return this.right.search(value);
}
}
// 添加结点的方法
// 递归的形式添加结点,注意需要满足二叉排序树的要求
public void add(Node node) {
if (node == null) {
return;
}
// 判断传入的结点的值,和当前子树的根结点的值关系
if (node.value < this.value) {
// 如果当前结点左子结点为null
if (this.left == null) {
this.left = node;
} else {
// 递归的向左子树添加
this.left.add(node);
}
} else { // 添加的结点的值大于 当前结点的值
if (this.right == null) {
this.right = node;
} else {
// 递归的向右子树添加
this.right.add(node);
}
}
//当添加完一个结点后,如果: (右子树的高度-左子树的高度) > 1 , 左旋转
if(rightHeight() - leftHeight() > 1) {
//如果它的右子树的左子树的高度大于它的右子树的右子树的高度
if(right != null && right.leftHeight() > right.rightHeight()) {
//先对右子结点进行右旋转
right.rightRotate();
//然后在对当前结点进行左旋转
leftRotate(); //左旋转..
} else {
//直接进行左旋转即可
leftRotate();
}
return ; //必须要!!!
}
//当添加完一个结点后,如果 (左子树的高度 - 右子树的高度) > 1, 右旋转
if(leftHeight() - rightHeight() > 1) {
//如果它的左子树的右子树高度大于它的左子树的高度
if(left != null && left.rightHeight() > left.leftHeight()) {
//先对当前结点的左结点(左子树)->左旋转
left.leftRotate();
//再对当前结点进行右旋转
rightRotate();
} else {
//直接进行右旋转即可
rightRotate();
}
}
}
/**
* 中序遍历
*/
public void infixOrder(){
if (this.left!=null){
this.left.infixOrder();
}
System.out.println(this);
if (this.right!=null){
this.right.infixOrder();
}
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
}
AVL树
/**
* 平衡二叉树
*/
public class AvlTree {
private Node root;
public Node getRoot() {
return root;
}
/**
* 查询
* @param value
* @return
*/
public Node search(int value){
if (root == null){
return null;
}
return root.search(value);
}
/**
* 根据value 查询节点的父节点
* @param value
* @return
*/
public Node searchParent(int value){
if (root == null ){
return null;
}
return root.searchParent(value);
}
/**
* 增加节点
* @param value
*/
public void add(int value){
Node node = new Node(value);
if (root == null){
root=node;
return;
}
root.add(node);
}
/**
* 中序遍历
*/
public void infixOrder(){
if (root != null){
root.infixOrder();
}
}
public static void main(String[] args) {
int[] arr = { 10, 11, 7, 6, 8, 9 };
AvlTree avlTree = new AvlTree();
for (int i = 0; i < arr.length; i++) {
avlTree.add(arr[i]);
}
avlTree.infixOrder();
}
}
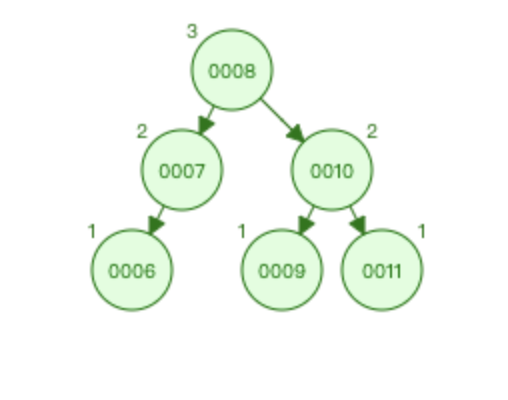
结果对比
原始的二叉排序树
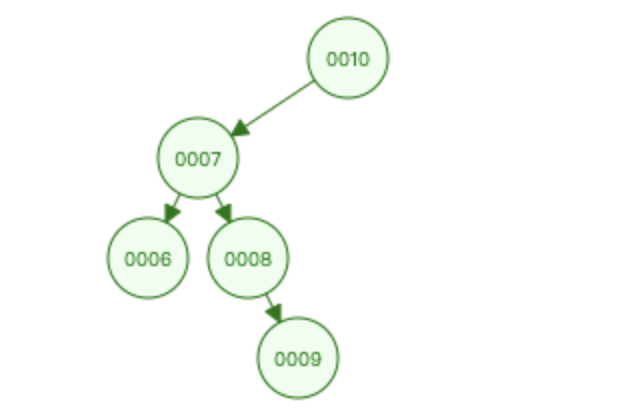
平衡二叉树(AVL树)


评论区