数据结构与算法（十二）排序--归并排序

归并排序介绍:

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

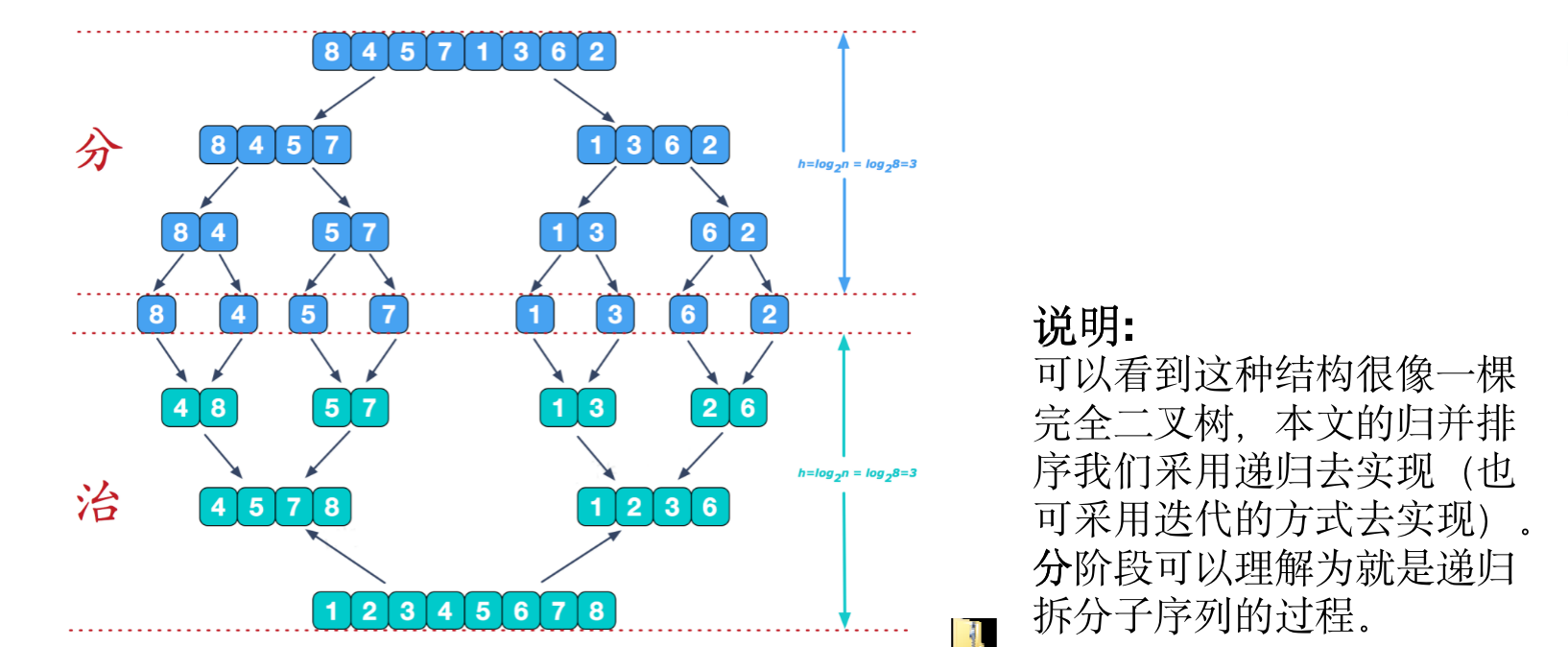
分而治之(divide - conquer);每个递归过程涉及三个步骤

第一, 分解: 把待排序的 n 个元素的序列分解成两个子序列, 每个子序列包括 n/2 个元素.

第二, 治理: 对每个子序列分别调用归并排序MergeSort, 进行递归操作

第三, 合并: 合并两个排好序的子序列,生成排序结果.

代码实现

/**
     * 分——合
     * @param arr
     * @param left
     * @param right
     * @param temp
     */
    public static void mergetSort(int [] arr,int left ,int right,int [] temp){

        if (right>left){
            int mid=(left+right)/2;
            mergetSort(arr,left,mid,temp);
            mergetSort(arr,mid+1,right,temp);
            merge(arr,left,mid,right,temp);

        }

    }

    /**
     * 合并的方法
     * @param arr
     * @param left
     * @param mid
     * @param right
     * @param temp
     */
    public static void merge(int [] arr,int left,int mid,int right,int [] temp){

        int i=left;
        int j=mid+1;
        int t=0;

        while (i<=mid&&j<=right){
            if (arr[i]<=arr[j]){
                temp[t++]=arr[i++];
            }else {
                temp[t++]=arr[j++];
            }
        }

        while (i<=mid){
            temp[t++]=arr[i++];
        }

        while (j<=right){
            temp[t++]=arr[j++];
        }

        t=0;
        int tempLeft=left;
        while (tempLeft<=right){
            arr[tempLeft++]=temp[t++];
        }

    }