从斐波那契数列中学习动态规划

斐波那契数列

斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)（n>=3，n∈N*）。 这是一个非常简单的问题，我们可以非常简单的找出Fn以及Fn-1与Fn-2的关系。 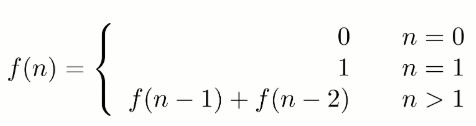看到这个公式我们首先想到用递归求解：

public int Fibonacci(int n) {
    if (n <= 1)
        return n;
    return Fibonacci(n-1)+Fibonacci(n-2);
}

但是这样写有一个特点就是会重复计算比如求F6会求出两次F4的值，其次如果递归的次数过多会报方法栈溢出。 然后进行改进使用动态规划（动态规划会把子问题的解缓存起来，从而避免重复求解子问题）：

public int Fibonacci(int n) {
    if (n <= 1)
        return n;
    int[] fib = new int[n + 1];
    fib[1] = 1;
    for (int i = 2; i <= n; i++)
        fib[i] = fib[i - 1] + fib[i - 2];
    return fib[n];
}

注意：如果明确表示了求Fn，则动态规划也可以省了则可以进行如下改进：

public int Fibonacci(int n) {
    if (n <= 1)
        return n;
    int pre2 = 0, pre1 = 1;
    int fib = 0;
    for (int i = 2; i <= n; i++) {
        fib = pre2 + pre1;
        pre2 = pre1;
        pre1 = fib;
    }
    return fib;
}